
FPGA是實現數字信號處理的一種高效手段。在實現高帶寬信號處理領域,FPGA技術可以通過一個芯片上的多級運算單元來獲得比通用DSP芯片更高的運算速度[2]。由于采樣率變換能用一種并行的方法實現,使用FPGA來實現就可以利用其硬件本身的并行性得到較高的效率。
1 有理數采樣率變換器的原理
從概念上講,采樣率變換器可以通過數/模轉換,再對模擬信號進行給定頻率的模/數轉換得到。在實際的系統中,通過在數字域利用抽取和內插運算實現是一種更為合理和有效的手段。
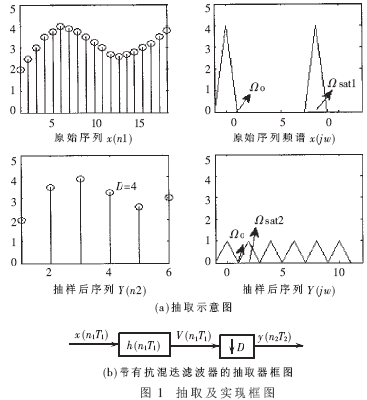
抽取是降低采樣率的方法。在時域上,D倍(D為抽取因子)抽取就是從原始序列中每隔D-1個樣點取出一個電感器生產構成新的數字序列。在頻域上,這一運算可以看成是頻譜的壓縮, 即原來以Ω sat1為周期的頻譜變為以Ω sat2為周期的頻譜。為避免可能引起的混迭失真,抽取前應使原信號通過一個低通濾波器。其抽取的示意圖及實現框圖如圖1所示。
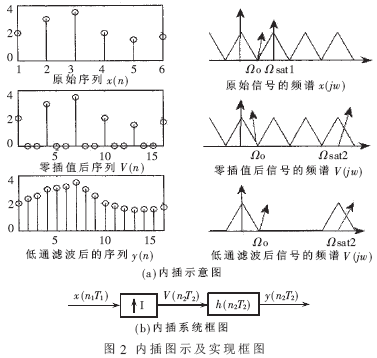
內插是提高采樣率的方法。實際的內插系統由兩部分構成:(1)零值插值器。設插值因子為I, I倍零值內插就是在原始序列任意兩個樣本間加入I-1個零值樣本。在頻域上,頻譜進行了擴張,即原來以Ω sat1為周期的頻譜變為以Ω sat2為周期的頻譜。從Ω c到Ω sat2-Ω c的頻帶被稱為鏡像頻譜。(2)低通濾波器。信號經過此濾波器后,鏡像頻譜被濾去,從而得到采樣率提高的信號序列。內插圖示及實現框圖如圖2所示。
利用抽取系統和內插系統的級連,就可以得到有理數采樣率轉換器的基本方案。一般地,對于 I/D 倍數的有理數采樣變換,通過先內插后抽取電感生產的方法,可以得到如圖3所示的實現框圖。圖3(a)中的第二部分和第三部分是兩個低通濾波器的級連,因而總的濾波效果等效為通帶邊緣較低的低通濾波器,合并后得到框圖3(b)。
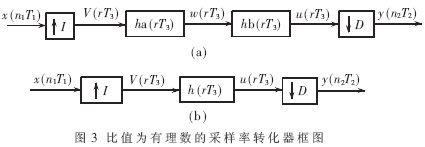
然而,對于上述三個系統,利用原始框圖直接實現并不是一個很好的方案。如從圖3可以看出,該系統最主要的運算量在濾波器的實現部分,圖3(b)中濾波器的采樣率為 F3=I,F1=DF2, 濾波運算是在最高采樣率的部分實現的,這是不經濟的。換一種說法,比如對后兩級的系統,經濾波后的序列每D個樣本中僅有一個是實際需要的,而D-1樣本的運算被丟棄了。
2 FIR濾波器的多相分解與多采樣率系統網絡變換
利用FIR濾波器的多相分解[1~2]及多采樣率系統網絡結構的變換[1],可以得到降低了運算代價的采樣率變換器的多相結構。
FIR濾波器的多相分解是指將數字濾波器H(z)可分解為若干個不同的組。設H(z)的轉移函數為:
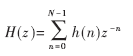
式中,N為濾波器長度,設N為D的整數倍, 即N/D=Q, Q為整數,可將沖激響應h(n)分成D個組,且有:
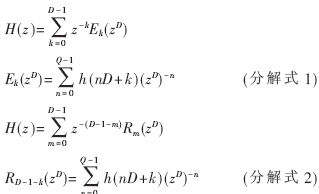
對于多采樣率網絡,存在下面幾個等效變換:
T1: 抽取與乘常數可以一體成型電感器換位。
T2: 零值插值和乘常數可以換位。
T3:兩個信號先分別抽取然后相加,以及先相加然后抽取等效。
T4:抽樣率相同的兩個信號先分別零值內插(內插因子相等)然后相加,以及先相加然后零值內插等效。
T5:如果I和D 互質,則抽取與內插可以交換。
此外,Nobel關系式[3]給出了抽取/電感器生產廠家內插與濾波器級連時如圖4所示的等效變換。
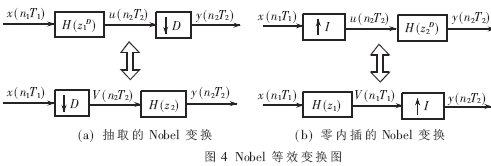
Nobel 關系式的意義在于:在抽取與濾波級連時,首先進行抽取運算,可以把濾波器的長度降低一個D因子; 內插與濾波級連時,首先進行濾波運算,可以使濾波器的的長度降低一個I因子。
大功率電感廠家 |大電流電感工廠